問題5.1

次の記号列はどれも文ではない．それぞれを文に変換せよ．ただし、量化子を加えたり，除いたりしてはいけない。

1. ∀x Cube(x) → Small(x)
2. ∃a Cube(a)
3. ∃v Cube(v) ∧ Medium(v) ∧ Larger(v, c)
4. ∃u (Small(u) ∧ Cube(u)
5. ∀w (Tet(w) → ∃z Dodec(z) ∧ Larger(w, z))
6. ∀x ∀y ∀z LeftOf(x, y) ∧ LeftOf(y, z) → LeftOf(x, z)
7. ∀x ∀y (Larger(a, b) → Cube(a) ∧ Dodec(b))
8. ∀x ∀y Cube(x) ∧ Cube(y) → LeftOf(x, y)
9. ∀x (Cube(x) → ∃x Between(x, x, y))

問題5.2

次の表現はどれも文ではない．量化子を加えるか除くことによって，それぞれを文に変換せよ．必要ならば変項も加えてよいが，カッコを加えてはいけない．

1. (Tet(w) → Large(w))
2. Tet(a) → Large(w)
3. Tet(w) → Large(w)
4. ∀x y ((Cube(x) ∧ Cube(y)) → ¬Larger(x, y))
5. ∀ Cube(a)
6. ∀x Tet(y) → Small(x)
7. ((Tet(x) ∧ Tet(y)) → Between(z, x, y))
8. (Tet(x) ∧ Large(x)) ∧ LeftOf(x, y)

問題5.3

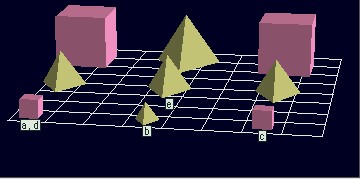
次の記号列のうち，良形式でないものは良形式に，良形式だが文でないものは文に変換せよ．また，はじめから文であるような記号列についても，下の絵に描かれた世界において真であるか判定し，偽である場合は真となるように書き換えよ．

1. Small(Cube(a)) FrontOf Tet(e)
2. (Cube(a))
3. ¬BackOf(x, b)
4. Cube(a) ∧ Cube(b) ∨ Cube(c)
5. Cube(a) <--> Cube(b) <--> Cube(e)
6. ∃x ¬(Cube x)
7. ∃a (Cube(a) ∧ Small(a))
8. ∃x Cube(x) ∧ Small(x)
9. ∃y (Tet(y) ∧ Large(y))
10. ∀y (Cube(x) → ¬Medium(x))
11. ∀x (Tet(x) ∧ Small(x) → FrontOf(x, e))
12. ∀u ((Tet(u) ∧ Medium(u)) → BackOf(u, c))

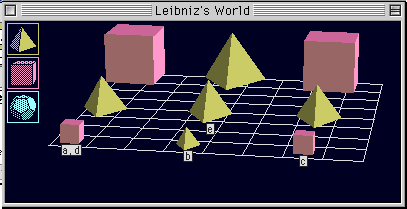
問題5.4

次の文のそれぞれについて，それが下の絵に描かれた世界において真であるかどうか判定せよ．

1. ∀x Cube(x)
2. ∀x ¬Dodec(x)
3. ∀x ¬Small(x)
4. ¬∀x Small(x)
5. ∃x Tet(x)
6. ∃x Dodec(x)
7. ∃x ¬Large(x)
8. ¬∃y Large(y)
9. ∃x BackOf(x, x)
10. ∀x (Cube(x) ∨ Tet(x))
11. ∀x (Cube(x) ∧ Tet(x))
12. ∀x (Large(x) → Cube(x))
13. ∀x (Medium(x) → Cube(x))
14. ∀x (Small(x) → Tet(x))
15. ∃x Tet(x) → ∃x Large(x)
16. ∃x (Tet(x) ∧ Large(x))
17. ¬∃x (Dodec(x) ∧ Small(x))
18. ∃y (Cube(y) ∧ Small(y))
19. ∃x (Medium(x) ∧ Tet(x))
20. ∀x ((Small(x) ∧ Large(x)) → Dodec(x))
21. ∃x Tet(x) ∧ ∃y Tet(y) ∧ ∃z Tet(z) ∧ ∃u Tet(u)
22. ∀x (Cube(x) <--> ¬Tet(x))
23. ∀x (Cube(x) <--> Large(x))
24. ∀x Cube(x) <--> ∀x Large(x)
25. ∀x Cube(x) <--> ∀y Cube(y)
26. ¬∀x Cube(x) <--> ∀x ¬Cube(x)
27. ¬∃y Tet(y) <--> ∃y ¬Tet(y)

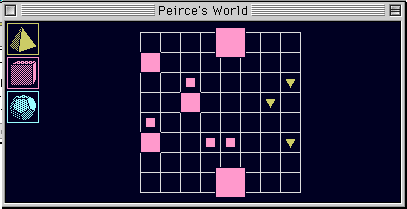
問題5.5

次の文のそれぞれについて，それが下の絵に描かれた世界において真であるかどうか判定せよ．

1. ∀x (x = a ∨ x = b ∨ x = c ∨ x = d)
2. ∃x (x ≠ a ∧ x ≠ b ∧ x ≠ c ∧ x ≠ d ∧ x ≠ e)
3. ∀x (x = a → x = d)
4. ∀x (Between(x, a, c) → x = b)
5. ∀x (¬∃y LeftOf(y, x) → x = a)
6. ∀x (Between(x, c, a) → x = b)
7. ∀x ((Tet(x) ∧ Small(x)) <--> x = b)

問題5.6

次の文はすべて，アリストテレスの範疇命題の形をしている．これらがすべて真になるような世界を描け．

1. ∃x (Tet(x) ∧ Large(x))
2. ∃x (Tet(x) ∧ Medium(x))
3. ∃x (Cube(x) ∧ ¬Small(x))
4. ∃y (Dodec(y) ∧ ¬Large(y))
5. ∀x (Cube(x) → Medium(x))
6. ∀x (Dodec(x) → Small(x))
7. ∀x (Tet(x) → ¬Small(x))
8. ∀y (Cube(y) → ¬Tet(y))

問題5.7

次の文のそれぞれについて，それが下の絵に描かれた世界において真であるかどうか判定せよ．

1. ∃x Tet(x)
2. ∃x (Tet(x) ∧ Large(x))
3. ∃x (Tet(x) ∨ Large(x))
4. ∃x ((Tet(x) ∧ ¬Tet(x)) ∨ Large(x))
5. ∃x (¬Tet(x) ∨ Large(x))
6. ∃x (Tet(x) → Large(x))
7. ∃x (Tet(x) ∧ Large(x) ∧ Large(x))
8. ∃x (¬Cube(x) ∨ Between(x, a, b))
9. ∃x (Cube(x) → Between(x, a, b))
10. ∃x (Cube(x) ∧ Between(x, a, b))

問題5.8

次の文がすべて真であると仮定して，それらに基づいて下の絵に描かれたブロックの名前を判定せよ．名前のない積み木もあるので注意．

1. Between(c, a, d) ∧ ¬Tet(c)
2. ∃x BackOf(x, a) ∧ ∃x FrontOf(x, c)
3. FrontOf(a, c) ∧ ¬∃x (BackOf(x, a) ∧ FrontOf(x, c))
4. ∃x LeftOf(x, d) <--> Large(b)
5. ∃x ∃y (¬Tet(x) ∧ ¬Tet(y) ∧ Between(b, x, y))
6. FrontOf(d, b) ∧ LeftOf(d, f)
7. Dodec(e)
8. ¬∃x LeftOf(x, e) ∨ Large(e)

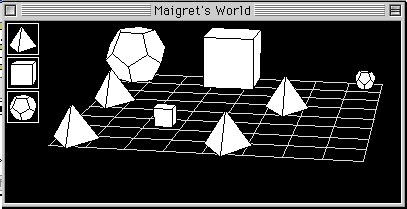
問題5.9

次の絵に描かれた世界を，1 から 8 の指示に従って，TW語で記述せよ．

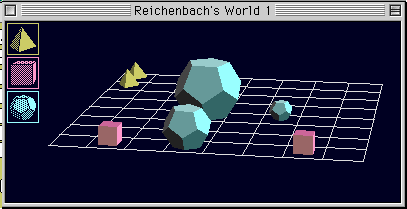
1. すべての四面体の大きさを記述する文を書け．
2. すべての立方体の大きさを記述する文を書け．
3. すべての１２面体は，小さいか，中位の大きさか，大きいかのどれかであるという事実を記述せよ．
4. この世界では，ある１２面体は中位の大きさであることに確認し，この事実を表現せよ．
5. ある１２面体は大きくないことを確認し，この事実を表現せよ．
6. ある１２面体は小さいを確認し，この事実を表現せよ．
7. ある１２面体は小さくないを確認し，この事実を表現せよ．
8. ある１２面体は大きくも，小さくもないを確認し，この事実を記述せよ．
9. どの四面体も大きくないという事実を記述せよ．
10. どの立方体も大きくないという点を記述せよ．

問題5.11

次の各文をTW語に翻訳せよ．それぞれ，∃ を一回使い，∀ は使わないはずである．まったく同じに翻訳される文もある点に留意せよ．さらに，翻訳された文の真理値を下に示した Montague's World 1, 2, 3, 4 で判定せよ．

1. Something is large.
2. Something is a cube.
3. Something is a large cube.
4. Some cube is large.
5. Some large cube is to the left of b.
6. A large cube is to the left of b.
7. b has a large cube to its left.
8. b is to the right of a large cube.［述語RightOfを使うこと．］
9. Something to the left of b is in back of c.
10. A large cube to the left of b is in back of c.
11. Some large cube is to the left of b and in back of c.
12. Some dodecahedron is not large.
13. Something is not a large dodecahedron.
14. It is not the case that something is a large dodecahedron.
15. b is not to the left of a cube.［この文はあいまいでなので，二つの可能な翻訳がある．一方は，∃ で始まり，他方は¬で始まる．真偽判定には，後者の解釈を用いること．］

問題5.12

文１〜４について，問に答えよ．

1. ∃x (Dodec(x) ∧ Large(x))
2. ∃x (Dodec(x) → Large(x))
3. ∀x (Tet(x) ∧ Small(x))
4. ∀x (Tet(x) → Small(x))

• これらの文のうち，Some dodecehedron is large の正しい翻訳になるものはどれか．All tetrahedra are small の正しい翻訳はどれか．（正しい翻訳の基準は，論理的同値性であることに注意．）
• 文２，４が真で，文１，３が偽であるような世界を描け．
• 文３が真で，文４が偽であるような世界は構成できるか？もしできるなら，その世界を描け．できないなら，その理由を説明せよ．
• 文１が真で，文２が偽であるような世界は構成できるか？もしできるなら，その世界を描け．できないなら，その理由を説明せよ．

問題5.13

文１〜５について，問に答えよ．

1. ∀x (Tet(x) → Large(x))
2. ∀x (Tet(x) → Medium(x))
3. ∀x (Tet(x) → Small(x))
4. ∀x (Tet(x) → (Small(x) ∧ Large(x)))
5. ∀x (Tet(x) → Cube(x))

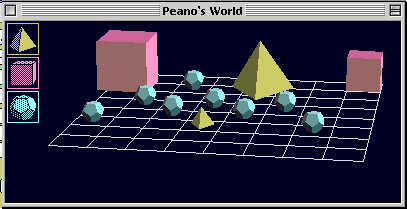
• Peano's World の中のどの積み木を消せば，文１は真になるか？
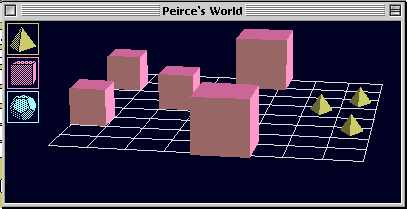
• Peirce's World の中のどの積み木を消せば，文１は真になるか？
• Peirce's World の中のそれらの積み木を消したと仮定せよ．その世界で，文２〜４の真理値を判定せよ．（空虚に真な一般化に注意せよ．）

問題5.14

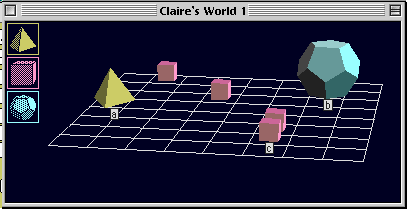
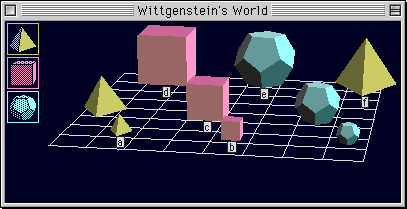
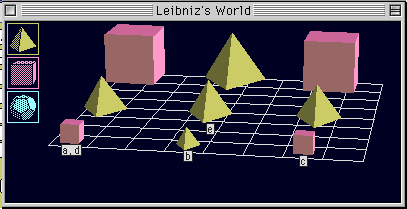
次の各文をTW語に翻訳せよ．それぞれ，∀ を一回使い，∃ は使わないはずである．さらに，Claire's World 1, Claire's World 2, Wittgenstein's World, Leibniz's World のそれぞれについて，各翻訳の真偽を判定せよ．

1. すべての立方体は小さい．
2. Each small cube is to the right of a.
3. すべての１２面体は大きい．
4. a は各１２面体の左にある．
5. Every medium tetrahedron is in fron of b.
6. 各立方体は b の前にあるか，a の後ろにあるかのどちらかである．
7. あらゆる立方体は，a の右にあり，また，b の左にある．
8. a と b の間にあるものはすべて立方体である．
9. Everything smaller than a is a cube.
10. すべての１２面体は小さくない．［この文はあいまいであると判断する人が多いので，可能な翻訳を二つとも記せ．一方は，∀ で始まり，他方は¬で始まるはずである．真偽判定の際には，この文が ∀ で始まる方の意味であると仮定すること．］
11. どのような１２面体も小さくない．
12. a はすべてのものの右にない．［この文はあいまいであると判断する人が多い．真偽判定の際には，¬で始まる方の意味であると仮定すること．］
13. a is not to the right of anything.
14. a is not to the right of any cube.
15. If something is a cube, the it is right of a and left of b.［この文は，something という名詞句を含んでいるが，∃ ではなく，∀ を使って翻訳されるべきである．］
16. Something is a cube if and only if it is right of a and left of b.

問題5.15

次の各文を TW語に翻訳し，さらに，前問で示した Leibniz's World に基づいて，その真偽を判定せよ．また，それらの文がすべて偽になるような世界にするためには，Leibniz's World をどのように変更すればよいか答えよ．

• b is a tetrahedron and is smaller than e.
• There are no medium sized cubes.
• Nothing is in front of b.
• Every cube is either in front of or in back of e.
• No cube is between a and c.

問題5.16

表１を使って，次の各文を一階述語言語に翻訳せよ．

1. People are not disks.
2. Disks are not people.
3. Silly was not erased at either 2:00 or 2:05.
4. Claire erased Folly sometime between 2:00 and 3:00.
5. Claire gave a disk to each and every student at 2:00.
6. Claire had only blank disks at 2:00.
7. Of all the students, only Claire was angry at 3:00.
8. No one erased Folly at 2:00.
9. If anyone erased Silly at 2:00, then they were angry.
10. Whoever owned Silly at 2:00 was angry five minutes later.

表１

英語	一階述語言語	注
名： Max Claire Folly Silly 2 pm, Jan 2, 1996 2:01 pm, Jan 2, 1996 :	Max Claire Folly Silly 2:00 2:01 :	特定のフロッピィーディスクの名 別のフロッピィーディスクの名 ある時刻の名 一分後の時刻の名 他の時刻についても同様
述語： x is a disk x is a person x is a student t is earlier than t' x was blank at time t x was angry at time t x owned y at time t x gave y to z at t x erased y at time t	Disk(x) Person(x) Student(x) t < t' Blank(x,t) Angry(x,t) Owned(x,y,t) Gave(x,y,z,t) Erased(x,y,t)	時間上の「よりも早い」という関係

問題5.17

前問の表１を使って次の文を自然な英語（もしくは日本語）に翻訳せよ．

1. ∀x(Person(y) → ¬Owned(y,Folly,2:00))
2. ¬∃x(Angry(x,2:00) ∧ Student(x) ∧ Erased(x,Folly,2:00))
3. ∀x(Person(x) ∧ Gave(Max,Folly,x,2:00)) → Angry(x,2:05))
4. ∀t¬Gave(Claire,Folly,Max,t)

問題5.18*

次の文をできるだけ忠実に一階述語言語に翻訳せよ．翻訳で用いた述語と関数記号の意味をすべて説明し，また，自分の翻訳の欠点についても，説明すること．

1. 勇気あるものだけが，許すことを知る．
2. No man is an island.
3. もしだれも私を愛さないなら，私もだれも愛さない．
4. Every nation has the government it deserves.
5. 確実なものなどない，論理以外は．
6. Misery (that is, a miserable person) loves company.　
7. すべて光るものが金であるわけではない．
8. あるところにおじいさんとおばあさんが住んでいました．
9. もし君がだれかれなしにほめるなら，君はだれもほめていないことになる．
10. デンマークの国では何かが腐っている．

問題5.19

ド・モルガンの法則を使って，「どのような P も Q ではい」の否定が「ある P は Q である」と論理的に同値であることを示せ．

問題5.20

文４〜６は，それぞれ，文１〜３のどれかと論理的に同値である．そのことをド・モルガンの法則を使って示せ．

1. ¬∀x (Cube(x) → Small(x))
2. ¬∃y (Cube(y) ∧ Large(y))
3. ¬∀x (Large(x) <--> Dodec(x))
4. ∀x (¬Large(x) ∨ ¬Cube(x))
5. ∃u (¬Small(u) ∧ Cube(u))
6. ∃x ((Large(x) ∧ ¬Dodec(x)) ∨ (Dodec(x) ∧ ¬Large(x)))

問題5.22

次の文がすべて真になるような世界を描け．

1. ∀x[Cube(x) → Large(x)]
2. ∀x[Large(x) → LeftOf(x,c)]
3. ∃x Cube(x)

問題5.23

以下は，前提１〜３から，∃x[Slithy(x) ∧ Mimsy(x)] を証明しようとした試みである．この証明は，正しいか？もし誤りがあれば，どこが誤っているか指摘し，正しい証明に直せ．

1. ∀x[(Brillig(x) ∨ Tove(x)) → (Mimsy(x) ∧ Gyre(x))]
2. ∀y[(Slithy(y) ∨ Mimsy(y)) → Tove(y)]
3. ∃x Slithy(x)

証明．前提３により，談話領域の中のあるものが slithy であることが分かっている．これらのものの一つを b 呼ぼう．前提２により，b は tove である．すると，前提１により，b は mimsy である．したがって，b は slithy で，かつ，mimsy である．したがって，あるものが slithy で，かつ，mimsy であることが導かれ，∃x[Slithy(x) ∧ Mimsy(x)] と結論できる．

問題5.24

以下は，前提１〜３から，∀z[Brillig(z) <--> Mimsy(z)] を証明しようとした試みである．この証明は，正しいか？もし誤りがあれば，どこが誤っているか指摘し，正しい証明に直せ．

1. ∀x[Brillig(x) → (Mimsy(x) ∧ Slithy(x))]
2. ∀y[(Slithy(y) ∨ Mimsy(y)) → Tove(y)]
3. ∀x[Tove(x) → (Outgrabe(x,b) ∧ Brillig(x))]

証明．以下の二点の連言は結論と論理的に同値なので，この２点をそれぞれ証明すれば十分である．

• ∀z[Brillig(z) → Mimsy(z)]
• ∀z[Mimsy(z) → Brillig(z)]

一般的条件証明の方法で，これらを順番に証明する．まず，Brillig であるような任意のものを b と呼ぶ．すると，前提１により，b は mimsy で，かつ，slithy である．したがって，それは mimsy である．よって，第一の点が導かれる． 第二の点を証明するために，mimsy であるような任意のものを b と呼ぶ．前提２により，b は tove である．すると，前提１により，b は brillig である．よって，第２の点が導かれる．

問題5.25

以下は，前提１〜３から，∃z Slithy(z) を証明しようとした試みである．この証明は，正しいか？もし誤りがあれば，どこが誤っているか指摘し，正しい証明に直せ．

1. ∀x[(Brillig(x) ∧ Tove(x)) → Mimsy(x)]
2. ∀y[(Tove(y) ∨ Mimsy(y)) → Slithy(y)]
3. ∃x Brillig(x) ∧ ∃x Tove(x)

証明．前提３により，birllig で tove であるものが存在することが分かる．これらのうちの一つを b と呼ぼう．前提１により，b は mimsy である．従って，前提２により，b が slithy であることが分かる．したがって，slithy であるものが存在することになり，∃z Slithy(z) と結論できる．

問題5.26

次の前提１〜３から，∃x Dodec(x) は導けるか？導けるのであれば，それを非形式的に証明せよ．導かれないのであれば，前提がすべて真で，結論が偽であるような世界を描け．

1. ∀y[Cube(y) ∨ Dodec(y)]
2. ∀x[Cube(x) → Large(x)]
3. ∃x ¬Large(x)

問題5.27

前問の前提１〜３から，∃x[Dodec(x) ∧ Small(x)] は導けるか？導けるのであれば，それを非形式的に証明せよ．導かれないのであれば，前提がすべて真で，結論が偽であるような世界を描け．

問題5.28

次の前提１〜３から，Small(c) は導けるか？導けるのであれば，それを非形式的に証明せよ．導かれないのであれば，前提がすべて真で，結論が偽であるような世界を描け．

1. ∀x[Cube(x) ∨ Dodec(x)]
2. ∀x[Cube(x) → (Large(x) ∧ LeftOf(c,x))]
3. ∀x[¬Small(x) → Tet(x)]

問題5.29

前問の前提１〜３から，Dodec(c) は導けるか？導けるのであれば，それを非形式的に証明せよ．導かれないのであれば，前提がすべて真で，結論が偽であるような世界を描け．

問題5.30

次の前提１〜２から，∃x[FrontOf(c,x) ∧ Cube(x)] は導けるか？導けるのであれば，それを非形式的に証明せよ．導かれないのであれば，前提がすべて真で，結論が偽であるような世界を描け．

1. ∀x[Cube(x) ∨ (Tet(x) ∧ Small(x))]
2. ∃x[Large(x) ∧ BackOf(x,c)]

問題5.31

前問の前提１〜２から，¬∃x[Small(x) ∧ BackOf(x,c)] は導けるか？導けるのであれば，それを非形式的に証明せよ．導かれないのであれば，前提がすべて真で，結論が偽であるような世界を描け．

問題5.32

次の各文を一階述語言語に翻訳し，さらに，４が１〜３から導けるかどうか答えよ．導けるなら，非形式的な証明を与えよ．

1. すべての子供は，右利きか賢いかのどちらかである．
2. 賢い子供はだれもレバーを食べない．
3. レバーもタマネギも食べる子供がいる．
4. タマネギを食べるような右利きの子供がいる．

問題5.33

問題5.16の文１，２は論理的に同値であるか？もしそうなら，それを非形式的に証明せよ．もしそうでないなら，なぜそうでないかを説明せよ．

問題5.35

¬∀xP(x) から ∃x¬P(x) を形式的に証明し，さらに，それに対応する非形式的証明を与えよ．

問題5.36

問題5.23で与えた非形式的証明に対応する形式的証明を与えよ．

問題5.37

問題5.25で与えた非形式的証明に対応する形式的証明を与えよ．

問題5.38

次の前提１〜３から，∃x Dodec(x) を形式的に証明せよ．

1. ∀y[Cube(y) ∨ Dodec(y)]
2. ∀x[Cube(x) → Large(x)]
3. ∃x¬Large(x)

問題5.39

次の１〜５のうち，いくつかは妥当で，いくつかは妥当でない．妥当であるものには，形式的証明を与え，妥当でないものについては，前提が真で結論が偽であるような世界を描け．

1. ∃x(Cube(x) ∧ Small(x)) という前提から，∃x Cube(x) ∧ ∃x Small(x) という結論．
2. ∃x Cube(x) ∧ ∃x Small(x) という前提から，∃x(Cube(x) ∧ Small(x)) という結論．
3. ∃x Cube(x) ∧ Small(d) という前提から，∃x(Cube(x) ∧ Small(x)) という結論．
4. ∀x(Cube(x) ∨ Small(x)) という前提から，∀x Cube(x) ∨ ∀x Small(x) という結論．
5. ∀x Cube(x) ∨ ∀x Small(x) という前提から，∀x(Cube(x) ∨ Small(x)) という結論．

問題5.40

次のそれぞれについて形式的な証明を与えよ．

1. ∀yP(y) という前提から，∀xP(x) という結論．
2. ∃yP(y) という前提から，∃xP(x) という結論．

問題5.41

次のそれぞれについて形式的な証明を与えよ．

1. ∃x¬P(x) という前提から，¬∀xP(x) という結論．
2. ∀x¬P(x) という前提から，¬∃xP(x) という結論．
3. ¬∃xP(x) という前提から，∀x¬P(x) という結論．

問題5.42

mother と father という関数記号をもつ一階述語言語を考える．次の表が，いろいろな人々の親子関係を表しているとする．

子	母	父
Claire	Mary	Jon
Melanie	Mary	Jon
Mary	Helen	Jim
Helen	Anna	William
Jon	Everlyn	Kenneth
Jim	Addie	Archie
Everlyn	Ellen	John

次の記号列はいずれも，x という自由変項をもつ原子良形式である．それぞれの良形式について，その式を x について満足するのは誰かを答えよ．満足するのが誰か判断不可能な場合は「判断不可能」と答えよ．

1. mother(x) = Ellen
2. father(x) = Jon
3. mother(father(x)) = Mary
4. father(mother(x)) = John
5. mother(father(x)) = Addie
6. father(mother(father(x))) = John
7. father(father(mother(x))) = Archie
8. father(father(Jim)) = x
9. father(father(mother(Claire))) = x

問題5.43

前問の表と下の表を参考にして，文１〜４の真偽を判定せよ．ただし，談話領域は下の表であげられた１４人の人物からなるとする．

人	身長	人	身長
Claire	４フィート２インチ	Melanie	５フィート２インチ
Addie	５フィート３インチ	Ellen	５フィート４インチ
Anna	５フィート７インチ	William	５フィート８インチ
Mary	５フィート６インチ	Helen	５フィート６インチ
Everlyn	５フィート７インチ	Archie	５フィート８インチ
Kenneth	５フィート１０インチ	Jim	６フィート０インチ
Jon	６フィート５インチ	John	５フィート１１インチ

1. ∃xTallerThan(x,mother(x))
2. ∃yTallerThan(mother(mother(y)),mother(father(y)))
3. ∀x[height(x) < 5 feet → TallerThan(father(x),Jim)]
4. ∀z[z ≠ father(Claire) → TallerThan(father(Claire),z)]

追加問題11.8

次の文のそれぞれについて，それが下の絵に描かれた世界において真であるかどうか判定せよ．

1. ∃x ∀y Smaller(x, y)

2. ∀x (Dodec(x) --> ∃y Smaller(x, y))
3. ∃x (Dodec(x) ∧ ∀y Smaller(x, y))
4. ∃y ∀x (Dodec(x) --> Smaller(x, y))
5. ∃y ∀x (Dodec(x) --> Smaller(y, x))
6. ∃y ∀x (Dodec(x) --> ¬Smaller(x, y))
7. ∀x ((Cube(x) ∧ Medium(x)) --> ¬∃y BackOf(y, x))
8. ∀x ((Cube(x) ∧ Medium(x)) --> ∃y ¬BackOf(y, x))
9. ∀x ((Cube(x) ∧ Large(x)) --> ¬∃y BackOf(y, x))
10. ∀x ((Cube(x) ∧ Large(x)) --> ∃y ¬BackOf(y, x))
11. ∃x (Tet(x) ∧ ∀y (Cube(y) --> BackOf(y, x)))
12. ∃x (Tet(x) ∧ ∀y (BackOf(y, x) --> Cube(y)))
13. ∃x (Cube(x) ∧ ∀y (Dodec(y) --> Smaller(y, x)))
14. ∃x (Cube(x) ∧ ∀y (Smaller(y, x) --> Dodec(y)))
15. ∀x ((Cube(x) ∧ ∃y LeftOf(x, y)) --> Large(x))
16. ∀x ((Tet(x) ∧ ∃y FrontOf(x, y)) --> Small(x))
17. ∀x (¬∃y BackOf(y, x) --> Cube(x))

追加問題11.9

次の文のそれぞれについて，それが下の絵に描かれた世界において真であるかどうか判定せよ．

1. ∀x (∃y (x = y) --> x = d)
2. ∀x ∀y ((Cube(x) ∧ Cube(y)) --> ∃z Between(z, x, y))
3. ∀x (Between(x, d, c) --> x = b)
4. ∀x (∃y Between(x, y, c) --> x = b)
5. ∀x (∃y Between(x, y, c) --> ¬Large(x))
6. ∀x (∃y ∃z Between(x, y, z) --> ¬Large(x))
7. ∀x (∃y ∃z Between(x, y, z) --> Tet(x))
8. ∀x (¬∃y LeftOf(y, x) --> x = a)
9. ∀x ((¬∃y LeftOf(y, x) ∧ ¬∃y FrontOf(y, x)) --> x = a)
10. ∀x (∃y ∃z (Between(x, y, z) ∧ Tet(y) ∧ Tet(z))
    --> x = e)
11. ∀x (∃y ∃z (Between(x, y, z) ∧ Cube(y) ∧ Cube(z))
    --> x = b)
12. ∀y (∃x ∃z (Between(x, y, z) ∧ x = b) -->
    (y = a | y = c))
13. ∀x ∀y ((Tet(x) ∧ Small(x) ∧ Tet(y) ∧ Small(y))
    --> x = y)
14. ∀x ∀y ((Dodec(x) ∧ Small(x) ∧ Dodec(y) ∧ Small(y))
15. ∀x (Dodec(x) --> x = b)
16. ∀x (Dodec(x) <--> x = b)
17. ∀x ((Tet(x) ∧ Small(x)) <--> x = b)
18. ∃y ∀x ((Tet(x) ∧ Small(x)) <--> x = y)
19. ∃y ∀x ((Cube(x) ∧ Small(x)) <--> x = y)