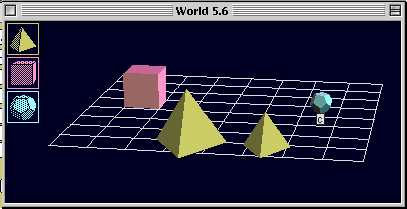
問題5.1

  1. ∀x (Cube(x) → Small(x))
  2. ∃x Cube(x)
  3. ∃v (Cube(v) ∧ Medium(v) ∧ Larger(v, c))
  4. ∃u (Small(u) ∧ Cube(u))
  5. ∀w (Tet(w) → ∃z (Dodec(z) ∧ Larger(w, z)))
  6. ∀x ∀y ∀z (LeftOf(x, y) ∧ LeftOf(y, z) → LeftOf(x, z))
  7. ∀x ∀y (Larger(a, b) → (Cube(a) ∧ Dodec(b)))
  8. ∀x ∀y ((Cube(x) ∧ Cube(y)) → LeftOf(x, y))
  9. ∀x (Cube(x) → ∃y Between(x, x, y))

　

問題5.2

  1. ∀w (Tet(w) → Large(w))
  2. Tet(a) → ∀w Large(w)
  3. ∀w Tet(w) → ∀w Large(w)
  4. ∀x ∀y ((Cube(x) ∧ Cube(y)) → ¬Larger(x, y))
  5. ∀x Cube(a)
  6. ∀y Tet(y) → ∀x Small(x)
  7. ∀x ∀y ∀z ((Tet(x) ∧ Tet(y)) → Between(z, x, y))
  8. ∃x (Tet(x) ∧ Large(x)) ∧ ∃x ∃y LeftOf(x, y)

　

問題5.3

  1. Small(a) ∧ (Cube(a)) ∧ FrontOf(a,e) ∧ Tet(e)
    （余分なカッコがあるが，それでも良形式である．）
  2. ∃x (Cube(x))
  3. ∃x ¬BackOf(x, b)
  4. Cube(a) ∧ (Cube(b) ∨ Cube(c))
  5. (Cube(a) <--> Cube(b)) <--> Cube(e)
  6. ∃x ¬(Cube (x))
  7. ∃x (Cube(x) ∧ Small(x))
  8. ∃x (Cube(x) ∧ Small(x))
  9. ∃y (Tet(y) ∧ Large(y))
    （真であるので，変更の必要なし．）
  10. ∀y (Cube(x) → ¬Medium(x))
    （真であるので，変更の必要なし．）
  11. ∀x ((Tet(x) ∧ Small(x)) → FrontOf(x, e))
  12. ∀u ((Tet(u) ∧ Medium(u)) → BackOf(u, c))
    （真であるので，変更の必要なし．）

　

問題5.4

  1. F
  2. T
  3. F
  4. T
  5. T
  6. F
  7. T
  8. F
  9. F
  10. T
  11. F
  12. T
  13. T
  14. F
  15. T
  16. F
  17. T
  18. T
  19. F
  20. T
  21. T
  22. T
  23. F
  24. T
  25. T
  26. F
  27. F

　

問題5.5

  1. F
  2. T
  3. T
  4. T
  5. F
  6. T
  7. T

　

問題5.6

問題5.7

  1. F
  2. F
  3. T
  4. T
  5. T
  6. T
  7. F
  8. T
  9. T
  10. F

　

問題5.8

省略＊．

　

問題5.9

  1. ∀x (Tet(x) → Small(x))
  2. ∀x (Cube(x) → Small(x))
  3. ∀x (Dodec(x) → (Small(x) ∨ Medium(x) ∨ Large(x))
  4. ∃x (Dodec(x) ∧ Medium(x))
  5. ∃x (Dodec(x) ∧ ¬Large(x))
  6. ∃x (Dodec(x) ∧ Small(x))
  7. ∃x (Dodec(x) ∧ ¬Small(x))
  8. ∃x (Dodec(x) ∧ ¬(Large(x) ∨ Small(x)))
  9. ∀x (Tet(x) → ¬Large(x))
  10. ∀x (Cube(x) → ¬Large(x))

　

問題5.10

  1. ∀x (Even(x) → ¬Prime(x))
  2. ∀x (Prime(x) → (Odd(x) ∨ x = 1+1)
  3. ∃x (Prime(x) ∧ Even(x))
  4. ∃x (Prime(x) ∧ ¬Even(x))

    2-4 は真．1 は偽．

　

問題5.11

  1. ∃x Large(x)
  2. ∃x Cube(x)
  3. ∃x (Large(x) ∧ Cube(x))
  4. ∃x (Cube(x) ∧ Large(x))
  5. ∃x (Large(x) ∧ Cube(x) ∧ LeftOf(x, b))
  6. ∃x (Large(x) ∧ Cube(x) ∧ LeftOf(x, b))
  7. ∃x (Large(x) ∧ Cube(x) ∧ LeftOf(x, b))
  8. ∃x (Large(x) ∧ Cube(x) ∧ RightOf(b, x))
  9. ∃x (LeftOf(x, b) ∧ BackOf(x, c))
  10. ∃x (Large(x) ∧ Cube(x) ∧ LeftOf(x, b) ∧ BackOf(x, c))
  11. ∃x (Large(x) ∧ Cube(x) ∧ LeftOf(x, b) ∧ BackOf(x, c))
  12. ∃x (Dodec(x) ∧ ¬Large(x))
  13. ∃x ¬(Dodec(x) ∧ Large(x))
  14. ¬∃x (Large(x) ∧ Dodec(x))
  15. ∃x (Cube(x) ∧ ¬LeftOf(b, x))　または ¬∃x (LeftOf(b, x) ∧ Cube(x))

Montague's 1

Montague's 2

Montague's 3

Montague's 4

1

T

T

F

T

2

T

T

T

T

3

T

T

F

F

4

T

T

F

F

5

T

F

F

F

6

T

F

F

F

7

T

F

F

F

8

T

F

F

F

9

T

T

T

F

10

T

F

F

F

11

T

F

F

F

12

T

T

T

F

13

T

T

T

T

14

T

T

T

F

15

T

F

F

F

　

問題5.12

省略．

　

問題5.13

　

問題5.14

  1. ∀x (Cube(x) → Small(x))
  2. ∀x ((Small(x) ∧ Cube(x)) → RightOf(x, a))
  3. ∀x (Dodec(x) → Large(x))
  4. ∀x (Dodec(x) → LeftOf(a, x))
  5. ∀x ((Medium(x) ∧ Tet(x)) → FrontOf(x, b))
  6. ∀x (Cube(x) → (FrontOf(x, b) ∨ BackOf(x, a)))
  7. ∀x (Cube(x) → (RightOf(x, a) ∧ LeftOf(x, b)))
  8. ∀x (Between(x, a, b) → Cube(x))
  9. ∀x (Smaller(x, a) → Cube(x))
  10. ∀x (Dodec(x) → ¬Small(x)) もしくは ¬∀x(Dodec(x) → Small(x))
  11. ∀x (Dodec(x) → ¬ Small(x))
  12. ¬∀x RightOf(a, x) もしくは ∀x ¬RightOf(a, x)
  13. ∀x ¬RightOf(a, x)
  14. ∀x (Cube(x) → ¬RightOf(a, x))
  15. ∀x (Cube(x) → (RightOf(x, a) ∧ LeftOf(x, b)))
  16. ∀x (Cube(x) <--> (RightOf(x, a) ∧ LeftOf(x, b)))

Claire's 1

Claire's 2

Wittgenstein's

Leibniz's

1

T

T

F

F

2

T

F

T

F

3

T

T

F

T

4

T

F

T

T

5

T

T

F

F

6

T

T

F

F

7

T

F

F

F

8

T

T

T

T

9

T

T

T

T

10

T

T

F

T

11

T

T

F

T

12

T

T

T

T

13

T

F

F

T

14

T

F

T

T

15

T

F

F

F

16

T

F

F

F

　

問題5.15

  1. Tet(b) ∧Smaller(b,e)
  2. ¬∃u (Medium(u) ∧ Cube(u))
  3. ¬∃u FrontOf(u,b)
  4. ∀w (Cube(w) → (FrontOf(w,e) ∨BackOf(w,e)))
  5. ¬∃u (Cube(u) ∧ Between(u,a,c))

真偽判定

  1. T
  2. T
  3. T
  4. T
  5. T

これらの文がすべて偽になるような世界にするためには、eとbの位置を入れ替え、その上で、b を中の大きさの立方体に変える。

　

問題5.16

省略＊．

　

問題5.17

（日本語にします．）

  1. ２時にフォリーを持っている人はいなかった．
  2. ２時にフォリーを怒って消した学生はいない．
  3. ２時にマックスからフォリーをもらったすべての人は，５分後に怒っていた．
  4. どの時間でも，クレアがマックスにフォリーをあげることはない．

　

問題5.18

省略．

　

問題5.19

No P's are Q's の否定は，¬∀x (P(x) → ¬Q(x)) に翻訳でき，Some P's are Q は，∃x (P(x) ∧ Q(x)) に翻訳できる．この二つの文は，次の変換によって論理的に同値である．

¬∀x (P(x) → ¬Q(x))
⇔∀x (¬P(x) ∨ ¬Q(x))　　 ［→ に関する同値関係］
⇔∃x ¬(¬P(x) ∨ ¬Q(x))　　［量化子に関するド・モルガンの法則］
⇔∃x (¬¬P(x) ∧ ¬¬Q(x))　　［ド・モルガンの法則］
⇔∃x (P(x) ∧ Q(x))　　［二重否定の法則］

　

問題5.20

∀x (Large(x) → ¬Cube(x))
⇔∀x (¬Large(x) ∨ ¬Cube(x))　　 ［→ に関する同値関係］
⇔∀x¬¬ (¬Large(x) ∨ ¬Cube(x))　　 ［二重否定の法則］
⇔¬∃x ¬(¬Large(x) ∨ ¬Cube(x))　　［量化子に関するド・モルガンの法則］
⇔¬∃x (¬¬Large(x) ∧ ¬¬Cube(x))　　［ド・モルガンの法則］
⇔¬∃x (Large(x) ∧ Cube(x))　　［二重否定の法則］
⇔¬∃y (Cube(y) ∧ Large(y))　　［∧の交換律］

∃u (¬Small(u) ∧ Cube(u))
⇔∃u ¬¬(¬Small(u) ∧ Cube(u))　　 ［二重否定の法則］
⇔¬∀x¬ (¬Small(u) ∧ Cube(u))　　 ［量化子に関するド・モルガンの法則］
⇔¬∀x(¬¬Small(u) ∨ ¬Cube(u))　　［ド・モルガンの法則］
⇔¬∀x(Small(u) ∨ ¬Cube(u))　　［二重否定の法則］
⇔¬∃x (¬Cube(u) ∨ Small(u))　　［∨の交換律］
⇔¬∀x (Cube(x) → Small(x))　　［→ に関する同値関係］

∃x (¬(Large(x) ∧ ¬Dodec(x)) → (Dodec(x) ∧ ¬Large(x)))
⇔∃x (¬¬(Large(x) ∧ ¬Dodec(x)) ∨ (Dodec(x) ∧ ¬Large(x)))
［→ に関する同値関係］
⇔∃x ((Large(x) ∧ ¬Dodec(x)) ∨ (Dodec(x) ∧ ¬Large(x)))
［二重否定の法則］
⇔∃x¬¬ ((Large(x) ∧ ¬Dodec(x)) ∨ (Dodec(x) ∧ ¬Large(x)))
［二重否定の法則］
⇔¬∀x¬ ((Large(x) ∧ ¬Dodec(x)) ∨ (Dodec(x) ∧ ¬Large(x)))
［量化子に関するド・モルガンの法則］
⇔¬∀x (¬(Large(x) ∧ ¬Dodec(x)) ∧ ¬(Dodec(x) ∧ ¬Large(x)))
［ド・モルガンの法則］
⇔¬∀x ((¬Large(x) ∨ ¬¬Dodec(x)) ∧ (¬Dodec(x) ∨ ¬¬Large(x)))
［ド・モルガンの法則］
⇔¬∀x ((¬Large(x) ∨ Dodec(x)) ∧ (¬Dodec(x) ∨ Large(x)))
［二重否定の法則］
⇔¬∀x ((Large(x) → Dodec(x)) ∧ (Dodec(x) → Large(x)))
［→ に関する同値関係］
⇔¬∀x (Large(x) <--> Dodec(x))　　［<-->に関する同値関係］

　

問題5.22

　

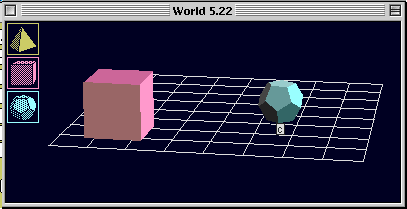
問題5.23

証明は正しい．各ステップと証明の方法をもっとはっきりさせると，次のようになる．

３番目の前提により，談話領域中の何らかの対象が slithy であることが分かっている．これらの対象の一つを b と名づけ，Slithy(b) と仮定する．２番目の前提と普遍例化により，(Slithy(b) ∨ Mimsy(b)) → Tove(d) である．しかし，Slithy(b) と仮定したから，当然，Slithy(b) ∨ Mimsy(b) であり，したがって，前件肯定により，Tove(d) である．すると，当然，Brillig(d) ∨ Tove(d) と言えるが，１番目の前提に普遍例化を適用すれば，(Brillig(d) ∨ Tove(d)) → (Mimsy(d) ∧ Gyre(d)) が得られ，前件肯定により，Mimsy(d) ∧ Gyre(d) である．すると，b は mimsy であり，また，仮定により slithy である．このように，少なくとも，我々が d と呼んだ対象については，Slithy(d) ∧ Mimsy(d) が成り立つから，（存在汎化により）∃x[Slithy(x) ∧ Mimsy(x)] と結論できる．

　

問題5.24

証明はほぼ正しいが，二度の普遍汎化の過程で導入されている名前が，前提ですでに使われている名前 b である点が，危険である．各ステップと証明の方法をはっきりさせながら，証明を修正すると次のようになる．

∀z[Brillig(z) <--> Mimsy(z)] を示すために，これと，論理的に同値な，∀z[Brillig(z) → Mimsy(z)] ∧ ∀z[Mimsy(z) → Brillig(z)] を示す．このためには，次の 4 と 5 を示せば十分である．

4. ∀z[Brillig(z) → Mimsy(z)]
5. ∀z[Mimsy(z) → Brillig(z)]

まず，一般条件証明によって 4 を導くために，c を談話領域の任意の対象を指す名前とし，Brillig(c) と仮定せよ．しかし，前提 1 に普遍例化を適用すれば，Brillig(c) → (Mimsy(c) ∧ Slithy(c)) となるから，前件肯定により，Mimsy(c) ∧ Slithy(c) が導ける．したがって，当然，Mimsy(c) である．このように，任意の対象 c について，Brillig(c) という仮定から，Mimsy(c) が導かれたから，4 であると結論できる．次に，一般条件証明によって 5 を導くために，e を談話領域の任意の対象を指す名前とし，Mimsy(e) と仮定せよ．すると，当然，Slithy(e) ∨ Mimsy(e) である．しかし，前提 2 に普遍例化を適用すれば，(Slithy(e) ∨Mimsy(e)) → Tove(e) となるから，前件肯定により，Tove(e) である．さらに，前提 3 に普遍例化を適用し，その結果に前件肯定を適用すれば，Outgrabe(e,b) ∧ Brillig(e) が得られる．したがって，当然，Brillig(e) である．このように，任意の対象 e について，Mimsy(c) という仮定から，Brillig(c) が導かれたから，5 であると結論できる．

　

問題5.25

証明は，前提 3 の使い方で間違っている．以下省略．

　

問題5.26

前提３により，談話領域内の何らかの対象が Large でないことが分かっている．存在例化による証明を行うために，これらの対象の一つを d と呼び，¬Large(d) と仮定する．前提 2 に普遍例化を適用すれば，Cube(d) → Large(d) である．したがって，Cube(d) と仮定すれば，前件肯定により Large(d) となってしまい，仮定に反するため，Cube(d) でないことが分かる．しかし，前提 1 と普遍例化によって，Cube(d) であるか，Dodec(d) であるかどちらかであることが導かれるから，Dodec(d) であることが分かる．このように，ここで d と呼んだ対象は少なくとも dodec であるから，∃xDodec(x) と結論できる．

　

問題5.27

導けない．下図参照．

　

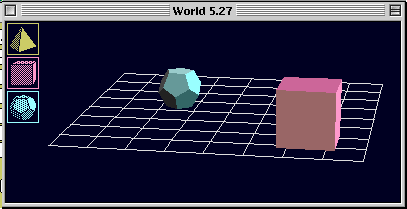
問題5.28

ヒント：導ける．この証明では，前提 2 は使わない．前提 1 と 3 に普遍例化を適用し，次の 1' と 3' を得たあと，背理法によって Small(c) を導く．

1'. Cube(c) ∨ Dodec(c)
3'. ¬Small(c) → Tet(c)

　

問題5.29

ヒント：導ける．この証明では，前提 3 は使わない．前提 1 と 2 に普遍例化を適用し，次の 1' と 3' を得たあと，Cube(c) でないことを示し，1' から Dodec(c) を結論する．

1'. Cube(c) ∨ Dodec(c)
3'. Cube(c) → (Large(c) ∧ LeftOf(c,c))

　

問題5.30

導ける．前提２が存在を主張している対象を d と呼び，Large(d) ∧ BackOf(d,c) と仮定する（存在例化)．これにより，Large(d) である．また，BackOf(d,c) でもあるので，明らかに，FrondOf(c,d) である．さて，前提１を d について普遍例化すれば，Cube(d) ∨ (Tet(d) ∧ Small(d)) が得られる．第１の場合として，Cube(d) と仮定すれば，先に得られた FrondOf(c,d) と合わせて，FrontOf(c,d) ∧ Cube(d) となり，存在汎化で，∃x[FrontOf(c,x) ∧ Cube(x)] となる．第２の場合として，Tet(d) ∧ Small(d) と仮定する．しかし，先に Large(d) が得られているから，明らかに矛盾する．つまり，第２の場合はあり得ない．よって，∃x[FrontOf(c,x) ∧ Cube(x)] と結論できる．［第２の場合の中で，背理法を使って，∃x[FrontOf(c,x) ∧ Cube(x)] を導いても構わない．証明は少し不格好になるけれども．］

　

問題5.31

省略＊．

　

問題5.32

  1. ∀x [Child(x) → (RightHanded(x) ∨ Clever(x))]
  2. ∀x [(Clever(x) ∧ Child(x)) → ¬EatLiver(x)]
  3. ∃x[Child(x) ∧ EatOnion(x) ∧ EatLiver(x)]
  4. ∃x[EatOnion(x) ∧ RightHanded(x) ∧ Child(x)]

４は１〜３から導ける．前提3により，レバーもタマネギも食べる子供がいることがわかるので，その対象を b と呼び， b はレバーもタマネギも食べる子供であると仮定する．前提1から， b が子供であれば， b は右利きか，賢いかのどちらかであるということが導ける（普遍例化）．b はこどもであるので，前件肯定により b は右利きか，賢いかのどちらかである．これをもとに， b が右利きであるということを場合による証明によって示す．まず， b が右利きであると仮定しよう．すると，当然， b は右利きである．次に， b が賢いと仮定しよう．背理法のために，さらに， b が右利きでないと仮定しよう．前提2から，b が賢い子供であれば， b はレバーを食べないということが導ける（普遍例化）．仮定により，b は賢いし， また，子供である．よって，b はレバーを食べない．しかし，これは，bがレバーを食べるという仮定に矛盾する．よって， b は右利きである．いずれの仮定からも， b が右利きであることが導かれたので， b は右利きであると結論してよい．すると， b はタマネギを食べるような右利きの子供であることになる．したがって，タマネギを食べるような右利きの子供が存在することになる．

 

問題5.33

ヒント：問題16 の文 1 と 文 2 は，それぞれ次のように翻訳できる．

1'. ∀x (Person(x) → ¬Disk(x))
2'. ∀x (Disk(x) → ¬Person(x))

したがって，文 1 と 文 2 が論理的に同値であることを示すためには，2' が 1' の論理的帰結であることと，1' が 2' の論理的帰結であることを示せばよい．どちらも，一般条件証明と背理法の組み合わせで容易に証明できる．

　

問題5.34

  1. 1+1 は素数であり，かつ偶数である．つまり，Prime(1+1) ∧ Even(1+1)．したがって，存在汎化により，∃x(Prime(x) ∧ Even(x))．
  2. 普遍汎化による証明のため，n を任意の自然数とし，Even(n) <--> Even(n2) であることを示す．このためには，次の 4 と 5 を示せば十分である．
      4. Even(n) → Even(n2)
      5. Even(n2) → Even(n)

    4 は明白である．5 を条件証明で示すために，Even(n2) と仮定する．背理法のため，¬Even(n) と仮定せよ．すると，ある自然数 m について，n = 2m+1 である．すると，n2 = (2m+1)2 = 2(2m2+2m)+1 であり，¬Even(n2) となって仮定に反するから，Even(n) であることが分かる．したがって，5 と結論できる．

  3. 一般条件証明のため，n を任意の自然数とし，Divisible(n2,3) と仮定せよ．背理法のため，¬Divisible(n2,9) と仮定せよ．すると，明らかに，¬Divisible(n,3) である．なぜなら，もし，Divisible(n,3) であれば，ある自然数 m について，n = 3m であり，n2 = 3(3m2 ) となり，¬Divisible(n2,9) という仮定に反するからである．しかし，¬Divisible(n,3) であるとすれば，ある自然数 k について，n = 3k+1 であるか，n = 3k+2 であるかのどちらかである．もし，n = 3k+1 であれば，n2 = 3(3m2+2m)+1 となり，¬Divisible(n2,3) である．もし，n = 3k+2 であれば，n2 = 3(3m2+4m+1)+1 となり，¬Divisible(n2,3) である．このように，どちらの場合も，¬Divisible(n2,3) が導かれ，仮定に反するので，背理法により，Divisible(n2,9) と結論できる．

　

問題5.35

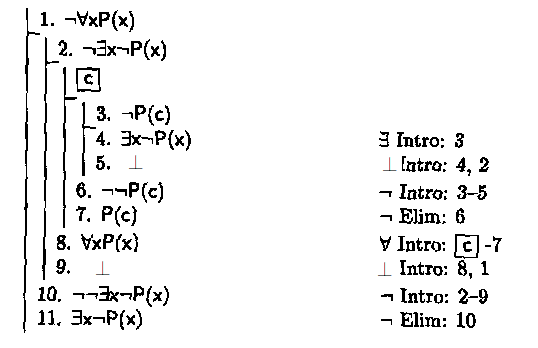
非形式的証明．∃x¬P(x) を背理法で示すために，¬∃x¬P(x) と仮定せよ．¬∀xP(x) が前提されているため，∀xP(x) が導ければ，矛盾になる．そこで，∀xP(x) の証明を試みる．そのためには，談話領域の任意の対象を c と呼び，P(c) を証明すればよい．ここで，背理法のために，¬P(c) であると仮定すれば，存在汎化により，∃x¬P(x) となる．これは，仮定 ∃x¬P(x) と矛盾する．よって，¬P(c) ではない．つまり，P(c) である．

　

問題5.36

　

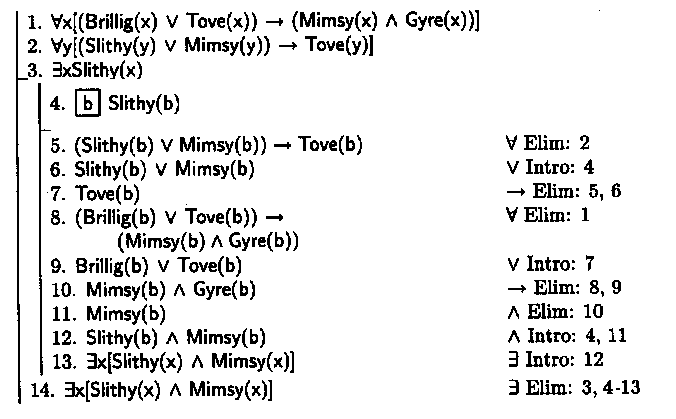
問題5.37

　

問題5.38

　

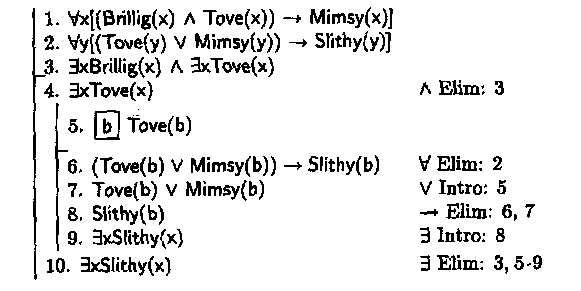
問題5.39

　

問題5.40

　

問題5.41

省略＊．

　

問題5.42

省略＊．

　

問題5.43

  1. True
  2. True
  3. True
  4. True

　

問題5.44

  1. ∀y¬Prime(y × y)
  2. ∃y¬Even(y × y)
  3. ∀y[1 < y → y < y × y]

すべて真である．

　

追加問題11.9

  1. F
  2. T
  3. F
  4. T
  5. F
  6. T
  7. T
  8. T
  9. F
  10. T
  11. T
  12. T
  13. T
  14. F
  15. T
  16. F
  17. T

　

追加問題11.10

  1. F
  2. F
  3. T
  4. F
  5. T
  6. F
  7. T
  8. F
  9. T
  10. T
  11. F
  12. T
  13. T
  14. T
  15. T
  16. F
  17. T
  18. T
  19. F