問題2.1

次の各原子文について，図に描かれた世界において真であるかどうか判定せよ．

Large(d) Large(c) Large(f) Medium(c) Medium(b) Medium(f) Larger(c, b) Larger(d, e) Larger(d, f) Larger(a, e) BackOf(b, e) BackOf(b, f) BackOf(f, a) LeftOf(b, a) LeftOf(a, b) LeftOf(a, a) RightOf(a, b) RightOf(b, d) Between(d, e, f) Between(e, d, f) Between(c, a, f) Between(c, d, b) Between(c, b, e) Between(c, c, c) Between(c, a, e)

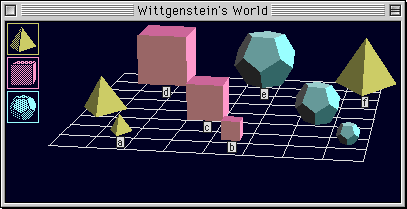問題2.2

次の各記号列がTW語の文であるか，文でないかを判定せよ．

1. Tet(a)
2. Medium(a)
3. Dodec(b)
4. Cube(c)
5. FrontOf(a,b)
6. Between(a,b,c)
7. a = d
8. Larger(a,b)
9. Smaller(a,c)
10. LeftOf(b,c)

問題2.3

問題2.2 で挙げたすべての文が真になるような世界を描け．

問題2.4

次の英語の文を，一階述語言語に翻訳せよ．

1. a is a cube.
2. b is smaller than a.
3. c is between a and d.
4. d is large.
5. e is larger than a.
6. b is a tetrahedron.
7. e is a dodecahedron.
8. e is right of b.
9. a is smaller than e.
10. d is in back of a.

さらに，それらの文がすべて真になるような世界を描け．

問題2.5

図に描かれている積み木に名前を付けよ．ただし，文１〜７がすべて真になるように，名前を付けること．

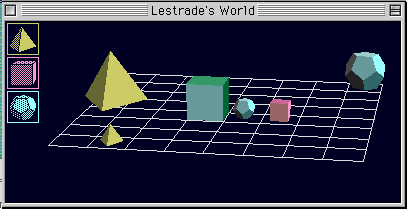
1. Dodec(a)
2. Dodec(b)
3. Cube(c)
4. Between(b, c, f)
5. LeftOf(d, c)
6. Smaller(f, a)
7. Larger(c, b)

問題2.6

問題2.5 で，可能な名前の付け方は何通りあるか？

追加問題1.12

次の各原子文の意味をできるだけ自然な日本語で表現せよ。

1. Taller(father(claire), father(max))
2. john = father(max)
3. Taller(claire, mother(mother(claire)))
4. Taller(mother(mother(max)), mother(father(max)))
5. mother(melanie) = mother(claire)

追加問題1.13

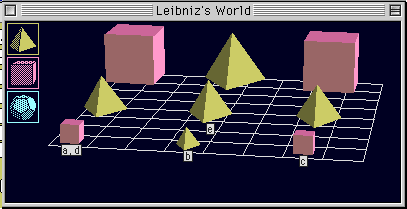
TW語に fm, bm, lm, rm という関数記号を加えたとすると、下記の1-10 はすべて TW 語の原子文と言える。それぞれの文が真であるか偽であるかを、図示した Leibniz's Worldについて判定せよ。

Tet(lm(e)) fm(c) = c bm(b) = bm(e) FrontOf(fm(e), e) LeftOf(fm(b), b) SameRow(rm(c), c) bm(lm(c)) = lm(bm(c)) SameShape(lm(b), bm(rm(e))) d = lm(fm(rm(bm(d)))) Between(b, lm(b), rm(b))

さらに、Bolzano's World について判定せよ。

Tet(lm(e)) fm(c) = c bm(b) = bm(e) FrontOf(fm(e), e) LeftOf(fm(b), b) SameRow(rm(c), c) bm(lm(c)) = lm(bm(c)) SameShape(lm(b), bm(rm(e))) d = lm(fm(rm(bm(d)))) Between(b, lm(b), rm(b))

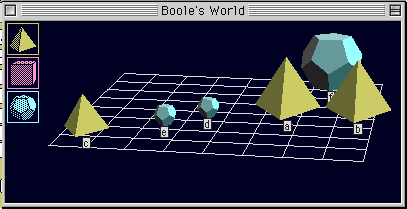
さらに、Booole's World について判定せよ。

Tet(lm(e)) fm(c) = c bm(b) = bm(e) FrontOf(fm(e), e) LeftOf(fm(b), b) SameRow(rm(c), c) bm(lm(c)) = lm(bm(c)) SameShape(lm(b), bm(rm(e))) d = lm(fm(rm(bm(d)))) Between(b, lm(b), rm(b))

さらに、Wittegenstein's World について判定せよ。

Tet(lm(e)) fm(c) = c bm(b) = bm(e) FrontOf(fm(e), e) LeftOf(fm(b), b) SameRow(rm(c), c) bm(lm(c)) = lm(bm(c)) SameShape(lm(b), bm(rm(e))) d = lm(fm(rm(bm(d)))) Between(b, lm(b), rm(b))

追加問題1.14

上記の原子文のうち、9以外のすべての文が偽になるような世界を描け。

問題2.9

父親という関係について話をするための一階述語言語を二通り考える．一方は，関数言語と呼ばれるもので，Claire, Melanie, Jon という名，father という関数記号，= と TallerThan という二つの述語記号を含んでいるとする．もう一方は，関係言語と呼ばれるもので，Claire, Melanie, Jon という名前，= という述語記号を含んでいるが，関数記号は含んでいないとせよ．次の各文は関係言語の原子文である．それぞれを，関数言語に翻訳せよ．（Claire = Calire といった原子文は，どちらの言語にも属する点に注意．そのような文は，それ自身の翻訳であると見なす．）

1. FatherOf(Jon,Claire)
2. FatherOf(Jon,Melanie)
3. TallerThan(Melanie,Claire)

次の各文は，関数言語の原子文である．どれが，関係言語に翻訳可能か？

1. father(Melanie) = Jon
2. father(Melanie) = father(Claire)
3. TallerThan(father(Claire),father(Jon))

追加問題1.17

人の背の高さの比較を表現するための一階述語言語を考案せよ．ただし，TallerThanなどの関係記号を使うのではなく，人の背の高さを指示するための関数記号と，= と < という二つの関係記号を使うこと．その言語では，少なくとも次のような情報を表現できなければならない．

• Carl is taller than Sam.
• Sam and Mary are the same height.

問題2.14

二つの異なった一階述語言語を考えよ．一方の言語は GaveScruffy(Claire,Claire) と GaveCarl(x,y) という二つの二項述語と Max と Claire という二つの名を含んでいる．他方は，Gave(x,y,z) という３項述語と，Max, Claire, Scruffy, Carl という名を含んでいる．

1. 一番目の言語で表現できる原子文をすべてすべてリストせよ．
2. 二番目の言語で表現できる原子文はいくつあるか．
3. 二番目の言語で表現できることをすべて一番目のような言語で表現しようとすると，いくつの名前と二項述語が必要であるか？

問題2.15

表１を使って，次の文を一階述語言語に翻訳せよ．時刻に言及する部分はすべて，１９９６年１月２日の時刻に言及しているとせよ．

1. Claire owned Folly at 2 pm.
2. Claire gave Silly to Max at 2:05 pm.
3. Max is a student.
4. Claire erased Folly at 2 pm.
5. Folly belonged to Max at 3:05 pm.
6. 2:00 pm is earlier than 2:05 pm.

表１

英語	一階述語言語	注
名： Max Claire Folly Silly 2 pm, Jan 2, 1996 2:01 pm, Jan 2, 1996 :	Max Claire Folly Silly 2:00 2:01 :	特定のフロッピィーディスクの名 別のフロッピィーディスクの名 ある時刻の名 一分後の時刻の名 他の時刻についても同様
述語： x is a disk x is a person x is a student t is earlier than t' x was blank at time t x was angry at time t x owned y at time t x gave y to z at t x erased y at time t	Disk(x) Person(x) Student(x) t < t' Blank(x,t) Angry(x,t) Owned(x,y,t) Gave(x,y,z,t) Erased(x,y,t)	時間上の「よりも早い」という関係

問題2.16

表１（問題2.15）を使って，次の一階述語言語を英語に翻訳せよ．（日本語でもいいよ．）

1. Owned(Max,Silly,2:00)
2. Erased(Max,Silly,2:30)
3. Gave(Max,Silly,Claire,2:00)
4. (2:00 < 2:00)

問題2.17*

次の各文を一階述語言語の原子文に翻訳して見よ．また，その際に使った名が，どのような類の対象を指示しているか明示し，また，使った述語の意味についても説明せよ．関数記号を使った場合は，その意味も説明せよ．

1. AIDS is less contagious than influenza.
2. Spain is between France and Portugal in size.
3. Misery loves company.
4. Max shook Claire's father's hand.
5. John and Nancy's eldest child is younger than Jon and Mary Ellen's.

問題2.18

同一者の不可識別性だけを使って，a = b と b = c から，a = c を証明せよ．

問題2.19

TW語に含まれる述語の意味が与えられたとき，次のうちどの結論が，先行する前提の論理的帰結であると言えるか答よ．結論が前提の帰結でない場合には，前提が真であるのに結論が偽であるような世界を描け．

1. 前提：LeftOf(a,b)　結論：RightOf(b,a)
2. 前提：LeftOf(a,b), b = c　結論：RightOf(c,a)
3. 前提：LeftOf(a,b), RightOf(c,a)　結論：LeftOf(b,c)
4. 前提：BackOf(a,b), FronfOf(a,c)　結論：FrontOf(b,c)
5. 前提：Between(b,a,c), LeftOf(a,c)　結論：LeftOf(a,b)　
   [ヒント：これはひっかけ問題．練習問題2.1を参照のこと．]

問題2.20

次の文を考えよ．

1. Folly was Claire's disk at 2 pm.
2. Silly was Max's disk at 2 pm.
3. Silly was not Claire's disk at 2 pm.

３は１と２から帰結するか．２は１と３から帰結するか？１は２と３から帰結するか？それぞれの場合について，もし答が「帰結しない」であれば，前提が真になり，結論が偽になるような可能な状況を記述せよ．

問題2.21

問題 2.18 で与えた証明を形式化せよ．

問題2.22

Likes(a,b), b = c, c = d を前提に，Likes(a,d) の形式的証明を与えよ．

問題2.23

Between(a,d,b), a = c, e = b を前提に，Between(c,d,e) の形式的証明を与えよ．

問題2.24

TW語に含まれる述語 Smaller は推移的である．すなわち，Smaller(a,c)　 は，Smaller(a,b) と Smaller(b,c) とから帰結する．

1. このことをフィッチ型の規則の形式で表現せよ．
2. その規則を使って，Smaller(a,b), Smaller(c,d), b = c を前提に，Smaller(a,d) の形式的証明を与えよ．

問題2.25

RightOf という述語と，LeftOf という述語の関係を表すフィッチ型の規則（複数可）を与えよ．その規則を使って，LeftOf(b,a) と b = c を前提にRightOf(a,c)を形式的に証明せよ．