A-3 Gauss 関数の積分
A-3.1 xe-ax2 の積分
この積分は,次の置換を用いることによって簡単に計算できる。
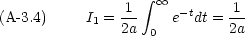
積分範囲が (-

,

) であるときは,被積分関数が奇関数なので,積分はゼロになる。
A-3.2 e-ax2 の積分
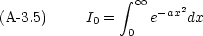
この積分は少々テクニックがいる。まず,この積分の二乗を考える。
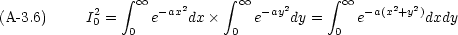
これは xy 平面上の二重積分である。次のような平面極座標に変数変換する。

すると
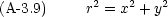
積分するときには次の注意が必要である。
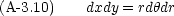
これは,図のように微小面積を求めればわかる。
式 (A-3.9), (A-3.10) を式 (A-3.6) に代入する。第一象限が積分範囲であることに注意すると
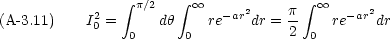
この積分は既に前節で行った。式 (
A-3.4) より
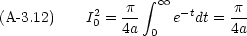
結局目的の積分は
積分範囲が (- ,
,  ) であるときは,被積分関数が偶関数なので,積分は I0 の 2 倍になる。
) であるときは,被積分関数が偶関数なので,積分は I0 の 2 倍になる。
A-3.3 xne-ax2 の積分
次のように置くことにする。
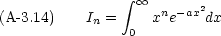
これを部分積分してみる。
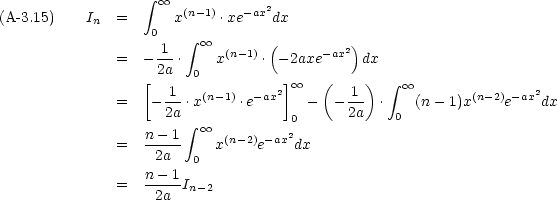
つまり,式 (
A-3.14) の形の積分は部分積分を繰り返すことによって,
n が偶数の場合には式 (
A-3.5) の積分に, n が 奇数の場合には式 (
A-3.1) の積分に帰着する。
積分範囲が (- ,
,  ) であるとき, n が偶数の場合は被積分関数が偶関数なので積分は In の 2 倍, n が奇数の場合は被積分関数が奇関数なので積分はゼロになる。
) であるとき, n が偶数の場合は被積分関数が偶関数なので積分は In の 2 倍, n が奇数の場合は被積分関数が奇関数なので積分はゼロになる。
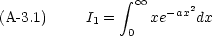

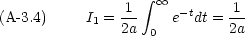
 ,
,  ) であるときは,被積分関数が奇関数なので,積分はゼロになる。
) であるときは,被積分関数が奇関数なので,積分はゼロになる。


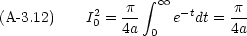
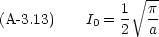
 ,
,  ) であるときは,被積分関数が偶関数なので,積分は I0 の 2 倍になる。
) であるときは,被積分関数が偶関数なので,積分は I0 の 2 倍になる。
 ,
,  ) であるとき, n が偶数の場合は被積分関数が偶関数なので積分は In の 2 倍, n が奇数の場合は被積分関数が奇関数なので積分はゼロになる。
) であるとき, n が偶数の場合は被積分関数が偶関数なので積分は In の 2 倍, n が奇数の場合は被積分関数が奇関数なので積分はゼロになる。