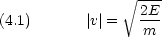
運動の周期 Tは
量子力学では,物理量に対応する演算子が重要な役割をはたす。
波動関数に演算子をはたらかせることにより,様々な量を計算することができる。
ここでは,一次元の箱の中の粒子の問題を例にして,演算子の用例を具体的に述べる。さらに,不確定性原理について簡単に触れる。
古典的な粒子(波動との二重性を持たない粒子)では,位置と運動量は独立した変数であり,常に確定した値を持っている。
実験手段の許す限り,いくらでも精密に測定できる。
ただし,測定をランダムに繰り返した場合には,粒子の状態の変化によって測定値にばらつきが生じる。
エネルギーが保存されている一次元の箱の中の粒子について,具体的に見てみる。粒子のエネルギーを E として
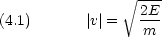
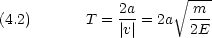
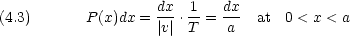
この確率密度は規格化されている。粒子の存在確率を全空間で積分すれば1なる。つまり,粒子は全空間のどこかに必ず 1個だけ存在する。
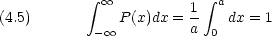
物理量 A の平均値<A>は,確率密度を使えば次のように書ける。
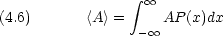
箱の中の粒子で位置の平均(期待値)を具体的に計算すると
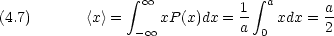
位置の分散(測定値がどれくらいばらつくかの目安)
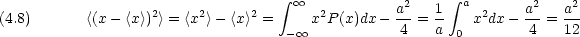
運動量の平均(p は x に無関係であることに注意せよ。また, p > 0 の値を持つ確率密度は P(x)/2,-p < 0 の値を持つ確率密度も P(x)/2である。)
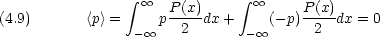
運動量の分散(この場合<p> = 0 なので,分散は 2 乗の平均に等しい。)
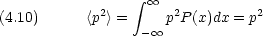
量子的な粒子(波動との二重性を持つ粒子)では,位置と運動量は独立した変数ではなく,
例えば位置を精密に決めようとすると運動量が判らなくなってしまう。
測定するためには粒子に光子をあてることが必要だが,光子が当たれば運動量が変わってしまう。
これは,単に測定方法の問題ではなく,量子的な粒子が原理的に持つ性質である。
位置の不確定性 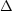 x と運動量の x 成分の不確定性
x と運動量の x 成分の不確定性 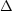 px の間には次の関係があることが知られている。
px の間には次の関係があることが知られている。
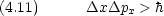
 と角運 動量 L にも同様の関係がある。
と角運 動量 L にも同様の関係がある。
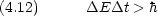
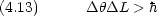
ただし,位置 x と運動量の y 成分 py の間にはこのような関係はない。
不確定性原理が成り立つのは,解析力学的に共役な変数の関係である。
(もう少し厳密にいえば,二つの演算子の順序を交換した場合に演算結果が等しくならない場合,その演算子に対応する物理量の間に不確定性原理が成り立つ。)
このような原理があるので,量子力学では確率が本質的に重要な役割をはたす。
全ての物事は,確率の世界で論じられているといってもよい。波動関数  (x) は,その確率と深い関係にある。
(x) は,その確率と深い関係にある。
粒子を x 〜 x + dx に見いだす確率の確率密度関数は次の式で表される。
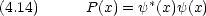
 *(x) は
*(x) は  (x) の複素共役。ただし,
(x) の複素共役。ただし,  (x) が実関数だったら
(x) が実関数だったら  *(x) =
*(x) =  (x) である。
(x) である。
規格化条件(意味するところは古典論と同じ)
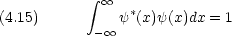
波動関数は,
一価(一つの x には  (x) の値が一つ)
(x) の値が一つ)
連続(この場合 2 回微分できる)
有界(規格化条件の積分が発散しない)
でなければならない。
量子力学では,物理量に対応する演算子がある。一次元空間中の質量 m の粒子については
| 物理量 | 記号 | 演算子 |
| 座標(位置) |  |
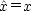 |
| 運動量 | 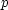 |
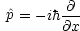 |
| 運動エネルギー | 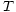 |
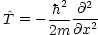 |
| ポテンシャルエネルギー | 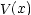 |
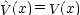 |
全エネルギーの演算子のことを特に Hamiltonian と呼び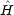 で表す。
で表す。
多次元多粒子系でも同様である。これは,古典的な解析力学で用いられる Hamiltonian関数 H (保存力場では全エネルギーと等しい)に由来する。
演算子とは,ある関数  にはたらかせるものである。例えば
にはたらかせるものである。例えば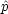
 は,
は,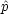 と
と  の掛け算ではなく,
の掛け算ではなく,
「 を x で偏微分して-ih を掛ける」という一連の操作を表している。
を x で偏微分して-ih を掛ける」という一連の操作を表している。
ただし,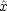 と
と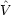 (x) の場合はたまたま,演算子をはたらかせることは x または V (x) を掛けることと同等である。
(x) の場合はたまたま,演算子をはたらかせることは x または V (x) を掛けることと同等である。
ある物理量の演算子は,位置と運動量の演算子から古典的類推で作られる。例えば運動エネルギー T は古典論で
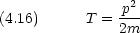
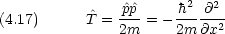
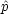 を 2回はたらかせることに変わったことに注意せよ。
を 2回はたらかせることに変わったことに注意せよ。
演算子は単に掛け算ではなく,数学的な操作を表しているので,表記する順序が重要である。
演算子は,必ず自分の右に書かれている関数に作用する。そして,複数の演算子がある場合には,右にあるものほど早く作用する。例えば次の二つ は全く違う。
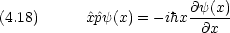
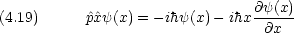
量子的な粒子について,ある物理量を測定する。一般には,測定値にはばらつきが生じる。
古典的な場合には,このばらつきは測定手段の不完全さによるが,量子的な場合にはより本質的原理的な問題による。
物理量を測定した場合の期待値は,波動関数と演算子から計算できる。測定する物理量を Q,演算子を![]() ,系の波動関数を
,系の波動関数を  (x) とすれば, Q の期待値は
(x) とすれば, Q の期待値は
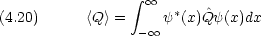
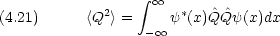
箱の中の粒子の問題で具体的に考える。
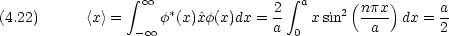
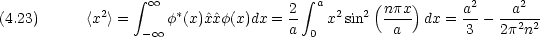
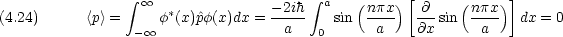
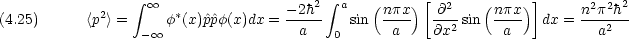
<x>と<p>とは古典的な場合と等しい。
<p2>は,古典論では任意の値をとれるが,量子論では離散的な値しかとることができない。
<x2>は, n が小さい場合には古典論から大きくずれるが, n が大きくなるにしたがって古典論の結果に近づいていく。
このような,量子数が大きくなるにしたがって古典論の結果に近づいていく現象は,一般的に見られる。
演算子Â について
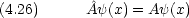
 (x) を固有関数という。
(x) を固有関数という。 dinger は Hamiltonian の固有値方程式である。
dinger は Hamiltonian の固有値方程式である。
 がÂ の固有関数であるとき,
がÂ の固有関数であるとき,  から計算した物理量Aの期待値<A>は固有値Aに等しい。
から計算した物理量Aの期待値<A>は固有値Aに等しい。
この場合, Aの測定を繰り返しても,原理的には同じ値になる。このような場合を「A が確定した値を持つ」という。
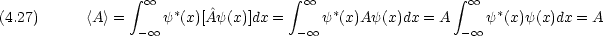
一次元の運動量演算子に関して固有値方程式を書く。
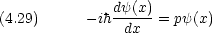
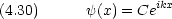

運動量が確定した値を持つということは,運動量の不確定性 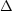 p がゼロということである。
p がゼロということである。
不確定性原理からすれば, この場合,位置の不確定性![]() x が無限大でなければならない。
x が無限大でなければならない。
現に,この  (x) は空間全体に均一拡がった波動を表しており,粒子の存在確率は至る所で同じである。
(x) は空間全体に均一拡がった波動を表しており,粒子の存在確率は至る所で同じである。
運動量演算子の固有関数は,運動エネルギー演算子の固有関数でもある。
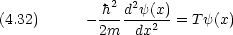
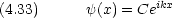
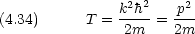
ところで,次の関数も運動エネルギー演算子の固有関数である。
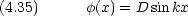
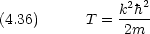
| (1) | e x x |
(  > 0, 0 < x < > 0, 0 < x < ) ) |
| (2) | e- x x |
(  > 0, 0 < x < > 0, 0 < x < ) ) |
| (3) | eim |
( 0 <  < 2 < 2 , m は整数, , m は整数,  は角度変数 ) は角度変数 ) |
| (4) | ei |
( 0 <  < 2 < 2 , ,  は整数ではない, は整数ではない,  は角度変数 ) は角度変数 ) |
| (5) | e- x x |
(  > 0, - > 0, - < x < < x < ) ) |
| (6) | e- x2 x2 |
(  > 0, - > 0, - < x < < x < ) ) |
 < x <
< x < でポテンシャル
でポテンシャル 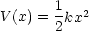 中を質量 m の粒子が運動する (kは定数 )。
中を質量 m の粒子が運動する (kは定数 )。
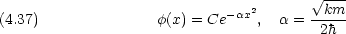
 1(x) と
1(x) と  2(x) がある。どちらの関数も x =
2(x) がある。どちらの関数も x =  及び x = -
及び x = - でゼロになるとする。
でゼロになるとする。
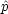 について次の関係を証明せよ。
について次の関係を証明せよ。 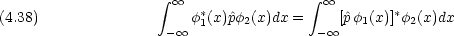
 (x) で表される系を考える。
(x) で表される系を考える。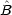 とがあるとき,交換子 [Â,
とがあるとき,交換子 [Â,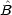 ] が次のように定義される。
] が次のように定義される。 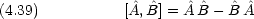
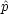 x と
x と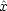
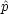 y と
y と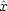
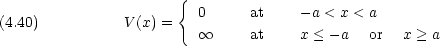
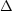 x
x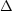 p を計算し,不確定性原理について考察せよ。
p を計算し,不確定性原理について考察せよ。